on
Generative adversarial networks
В прошлой статье мы рассмотрели порстейшую линейную генеративную модель PPCA. Вторая генеративная модель, которую мы рассмотрим — Generative Adversarial Networks, сокращенно GAN. В этой статье мы рассмотрим самую базовую версию этой модели, оставив продвинутые версии и сравнение с другими подходами в генеративном моделировании на следующие главы.
История
Генеративное моделирование предполагает аппроксимацию невычислимых апостериорных распределений. Из-за этого большинство эффективных методов, разработанных для обучения дискриминативных моделей, не работают с генеративными моделями. Существующие в прошлом методы для решения этой задачи вычислительно трудны и, в основном, основаны на использовании Markov Chain Monte Carlo, который плохо масштабируем. Поэтому для обучения генеративных моделей нужен был метод, основанный на таких масштабируемых техниках, как Stochastic Gradient Descent (SGD) и backpropagation. Один из таких методов — Generative Adversarial Networks (GAN). Впервые GANы были предложены в этой статье в 2014 году. Высокоуровнево эта модель может быть описана, как две подмодели, которые соревнуются друг с другом, и одна из этих моделей (генератор), пытается научиться в некотором смысле обманывать вторую (дискриминатор). Для этого генератор генерирует случайные объекты, а дискриминатор пытается отличить эти сгенерированные объекты от настоящих объектов из тренировочной выборки. В процессе обучения генератор генерирует все более похожие на выборку объекты и дискриминатору становится все сложнее отличить их от настоящих. Таким образом, генератор превращается в генеративную модель, которая генерирует объекты из некого сложного распределения, например, из распределения фотографий человеческих лиц.
Модель
Для начала введем необходимую терминологию. Через $X$ мы будем обозначать некоторое пространство объектов. Например, картинки $64\times 64\times 3$ пикселя. На некотором вероятностном пространстве $\Omega$ задана векторная случайная величина $x : \Omega \to X$ с распределением вероятностей, имеющим плотность $p(x)$ такую, что подмножество пространства $X$, на котором $p(x)$ принимает ненулевые значения — это, например, фотографии человеческих лиц. Нам дана случайная i.i.d. выборка фотографий лиц для величины ${x_i, i \in [1, N], x_i \sim p(x)}$. Дополнительно определим вспомогательное пространство $Z=R^n$ и случайную величину $z:\Omega \to Z$ с распределением вероятностей, имеющим плотность $q(z)$. $D:X \to (0,1)$ — функция-дискриминатор. Эта функция принимает на вход объект $x \in X$ (в нашем примере — картинку соответствующего размера) и возвращает вероятность того, что входная картинка является фотографией человеческого лица. $G: Z \to X$ — функция-генератор. Она принимает значение $z \in Z$ и выдает объект пространства $X$, то есть, в нашем случае, картинку.
Предположим, что у нас уже есть идеальный дискриминатор $D$. Для любого примера $x$ он выдает истинную вероятность принадлежности этого примера заданному подмножеству $X$, из которого получена выборка ${x_i}$. Переформулируя задачу обмана дискриминатора, на вероятностном языке мы получаем, что необходимо максимизировать вероятность, выдаваемую идеальным дискриминатором на сгенерированных примерах. Таким образом оптимальный генератор находится как $G^{*}=\arg \max_G E_{z \sim q(x)} D_k\left(G\left(z\right)\right)$. Так как $\log(x)$ — монотонно возрастающая функция и не меняет положения экстремумов аргумента, эту формулу можно переписать в виде $G^{*}=\arg \max_G E_{z \sim q(x)} \log D_k\left(G\left(z\right)\right)$, что будет удобно в дальнейшем.
В реальности обычно идеального дискриминатора нет и его надо найти. Так как задача дискриминатора — предоставлять сигнал для обучения генератора, вместо идеального дискриминатора достаточно взять дискриминатор, идеально отделяющий настоящие примеры от сгенерированных текущим генератором, т.е. идеальный только на подмножестве $X$, из которого генерируются примеры текущим генератором. Эту задачу можно переформулировать, как поиск такой функции $D$, которая максимизирует вероятность правильной классификации примеров как настоящих или сгенерированных. Это называется задачей бинарной классификации и в данном случае мы имеем бесконечную обучающую выборку: конечное число настоящих примеров и потенциально бесконечное число сгенерированных примеров. У каждого примера есть метка: настоящий он или сгенерированный. В первой статье было описано решение задачи классификации с помощью метода максимального правдоподобия. Давайте распишем его для нашего случая.
Итак, наша выборка $S={(x, 1), x \sim p(x)} \cup {(G(z), 0), z \sim q(z) }$. Определим плотность распределения $f(\xi|\eta=1)=D(\xi), f(\xi|\eta=0)=1−D(\xi)$, тогда $f(\xi|\eta)$ — это переформулировка дискриминатора $D$, выдающего вероятность класса $1$ (настоящий пример) в виде распределения на классах ${0, 1}$. Так как $D(\xi) \in (0, 1)$, это определение задает корректную плотность вероятности. Тогда оптимальный дискриминатор можно найти как: \begin{equation} D^{*}=f^{*}(\xi|\eta)=\arg \max_{f} f(\xi_1,...|\eta_1,...)=\arg \max_{f} \prod_i f(\xi_i|\eta_i) \end{equation} Сгруппируем множители для $\eta_i=0$ и $\eta_i=1$:
\begin{equation} D^{*}=\arg \max_{f} \prod_{i, \eta=1} f\left(\xi_i|\eta_i=1\right) \prod_{i, \eta=0} f\left(\xi_i|\eta_i=0\right)= \end{equation} \begin{equation} =\arg \max_{D} \prod_{x_i \sim p(x)} D\left(x_i \right) \prod_{z_i \sim q(z)} \left(1−D\left(G\left(z_i\right)\right)\right)= \end{equation} \begin{equation} =\arg \max_{D} \sum_{x_i \sim p(x)} \log D\left(x_i\right) + \sum_{z_i \sim q(z)} \log \left(1−D\left(G\left(z_i\right)\right)\right) \end{equation}
И при стремлении размера выборки в бесконечность, получаем: \begin{equation} D^{*}=\arg \max_{D}E_{x_i \sim p(x)} \log D\left(x_i\right) + E_{z_i \sim q(z)} \log \left(1−D\left(G\left(z_i\right)\right)\right) \end{equation}
Итого, получаем следующий итерационный процесс:
- Устанавливаем произвольный начальный $G_0(z)$.
- Начинается $k$-я итерация, $k = 1...K$.
- Ищем оптимальный для текущего генератора дискриминатор: $D_k=\arg \max_{D}E_{x_i \sim p(x)} \log D\left(x_i\right) + E_{z_i \sim q(z)} \log \left(1−D\left(G_{k−1}\left(z_i\right)\right)\right)$
- Улучшаем генератор, используя оптимальный дискриминатор: $G_k=\arg \max_G E_{z \sim q(x)} \log D_k\left(G\left(z\right)\right)$. Важно находиться в окрестности текущего генератора. Если отойти далеко от текущего генератора, то дискриминатор перестанет быть оптимальным и алгоритм перестанет быть верным.
- Задача обучения генератора считается решенной, когда $D_k(x)=1/2$ для любого $x$. Если процесс не сошелся, то переходим на следующую итерацию в пункт (2).
В оригинальной статье этот алгоритм суммаризируется в одну формулу, задающую в некотором смысле минимакс-игру между дискриминатором и генератором: \begin{equation} \min_G \max_D L(D, G) = E_{x \sim p(x)} \log D(x) + E_{z \sim q(z)} \log \left(1−D\left(G\left(z\right)\right)\right) \end{equation}
Обе функции $D, G$ могут быть представлены в виде нейросетей: $D(x) = D(x, \theta_1), G(z)=G(z, \theta_2)$, после чего задача поиска оптимальных функций сводится к задаче оптимизации по параметрам и ее можно решать с помощью традиционных методов: backpropagation и SGD. Дополнительно, так как нейросеть — это универсальный аппроксиматор функций, $G(z, \theta_2)$ может приблизить произвольное распределение вероятностей, что снимает вопрос выбора распределения $q(z)$. Это может быть любое непрерывное распределение в некоторых разумных рамках. Например, $Uniform(−1,1)$ или $N(0, 1)$. Корректность этого алгоритма и сходимость $G(z)$ к $p(x)$ при достаточно общих предположениях доказана в оригинальной статье.
Нахождение параметров нормального распределения
С математикой мы разобрались, давайте теперь посмотрим, как это работает. Допустим, $X=R$, т.е. решаем одномерную задачу. $p(x)=N(\mu, \sigma), q(z)=N(0, 1)$. Давайте использовать линейный генератор $G(z, \theta)=a z + b$, где $\theta={a, b}$. Дискриминатор будет полносвязной трехслойной нейронной сетью с бинарным классификатором на конце. Решением этой задачи является $G(z, \mu, \sigma)=\mu z + \sigma$, то есть, $a=\mu, b=\sigma$. Попробуем теперь запрограммировать численное решение этой задачи с помощью Tensorflow. Полный код можно найти тут, в статье же освещены только ключевые моменты.
Первое, что нужно задать, это входную выборку: $p(x)=N(\mu, \sigma)$. Так как обучение идет на минибатчах, мы будем за раз генерировать вектор чисел. Дополнительно, выборка параметризуется средним и стандартным отклонением.
def data_batch(hparams):
"""
Input data are just samples from N(mean, stddev).
"""
return tf.random_normal(
[hparams.batch_size, 1], hparams.input_mean, hparams.input_stddev)
Теперь зададим случайные входы для генератора $q(z)=N(0,1)$:
def generator_input(hparams):
"""
Generator input data are just samples from N(0, 1).
"""
return tf.random_normal([hparams.batch_size, 1], 0., 1.)
Определим генератор. Возьмем абсолютное значение второго параметра для придания ему смысла стандартного отклонения:
def generator(input, hparams):
mean = tf.Variable(tf.constant(0.))
stddev = tf.sqrt(tf.Variable(tf.constant(1.)) ** 2)
return input * stddev + mean
Создадим вектор реальных примеров:
real_input = data_batch(hparams)
И вектор сгенерированных примеров:
generator_input = generator_input(hparams)
generated = generator(generator_input)
Теперь прогоним все примеры через дискриминатор. Тут важно помнить о том, что мы хотим не два разных дискриминатора, а один, потому Tensorflow нужно попросить использовать одни и те же параметры для обоих входов:
with tf.variable_scope("discriminator"):
real_ratings = discriminator(real_input, hparams)
with tf.variable_scope("discriminator", reuse=True):
generated_ratings = discriminator(generated, hparams)
Функция потерь на реальных примерах — это кросс-энтропия между единицей (ожидаемым ответом дискриминатора на реальных примерах) и оценками дискриминатора:
loss_real = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
labels=tf.ones_like(real_ratings),
logits=real_ratings))
Функция потерь на поддельных примерах — это кросс-энтропия между нулем (ожидаемым ответом дискриминатора на поддельных примерах) и оценками дискриминатора:
loss_generated = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
labels=tf.zeros_like(generated_ratings),
logits=generated_ratings))
Функция потерь дискриминатора — это сумма потерь на реальных примерах и на поддельных примерах:
discriminator_loss = loss_generated + loss_real
Функция потерь генератора — это кросс-энтропия между единицей (желаемым ошибочным ответом дискриминатора на поддельных примерах) и оценками этих поддельных примеров дискриминатором:
generator_loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
labels=tf.ones_like(generated_ratings),
logits=generated_ratings))
К функции потерь дискриминатора опционально добавляется L2-регуляризация.
Обучение модели сводится к поочередному обучению дискриминатора и генератора в цикле до сходимости:
for step in range(args.max_steps):
session.run(model.discriminator_train)
session.run(model.generator_train)
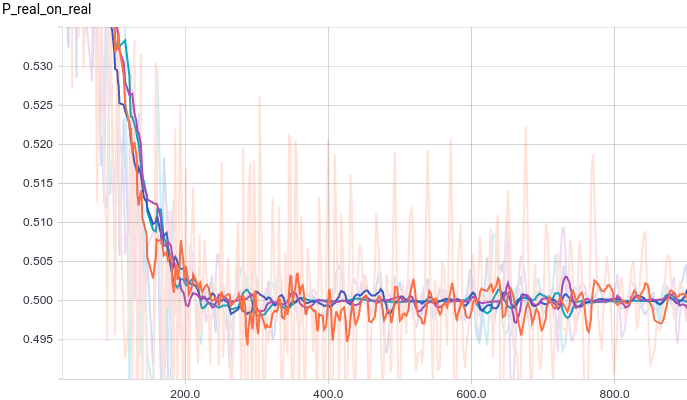
Ниже приведены графики для четырех моделей дискриминатора:
- трехслойная нейронная сеть.
- трехслойная нейронная сеть с L2-регуляризацией.
- трехслойная нейронная сеть с dropout-регуляризацией.
- трехслойная нейронная сеть с L2- и dropout-регуляризацией.
 |
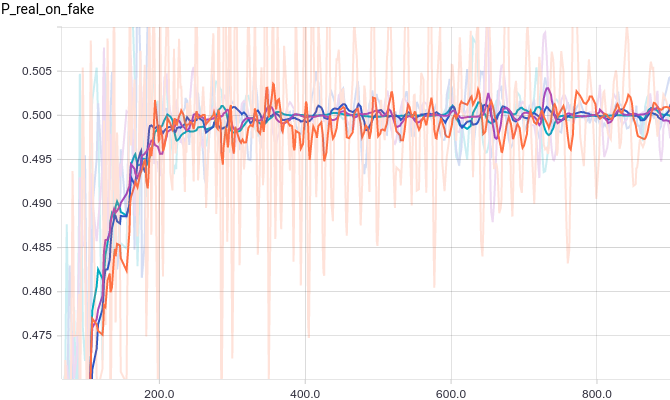 |
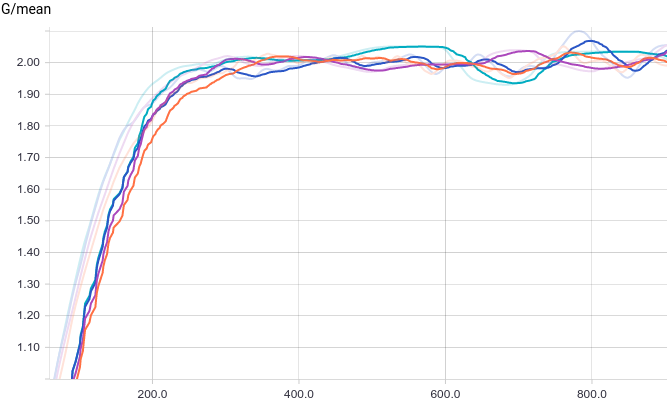
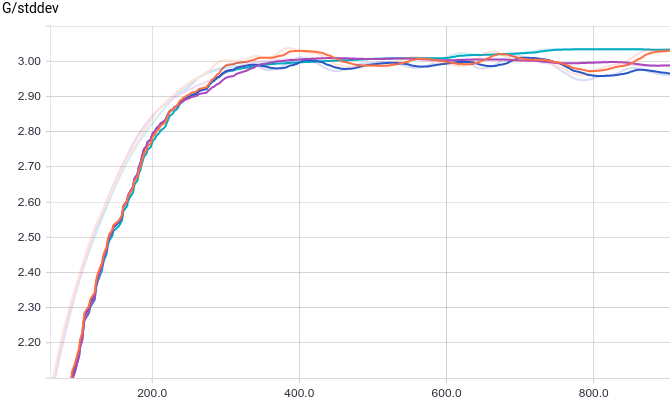
Все четыре модели достаточно быстро сходятся к тому, что дискриминатор выдает $1/2$ на всех входах. Из-за простоты задачи, которую решает генератор, между моделями почти нет разницы. Из графиков видно, что среднее и стандартное отклонение довольно быстро сходятся к значениям из распределения данных:
 |
 |
Ниже приведены распределения настоящих и сгенерированных примеров в процессе обучения. Видно, что сгенерированные примеры к концу обучения практически не отличимы от настоящих (они отличимы на графиках потому, что Tensorboard выбрал разные масштабы, но, если посмотреть на значения, то они одинаковые).
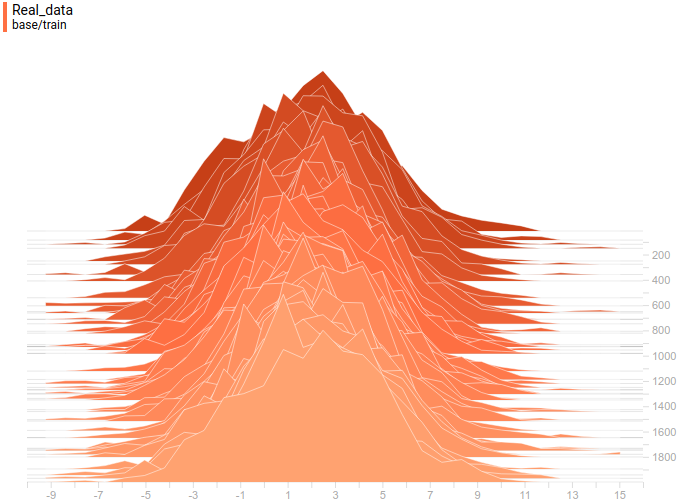 |
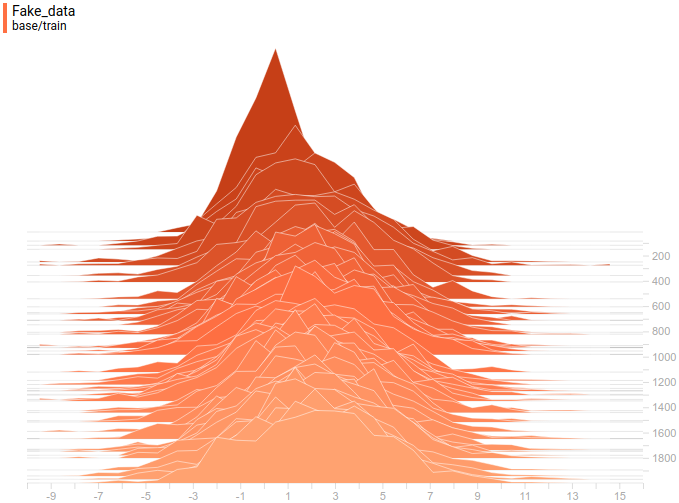 |
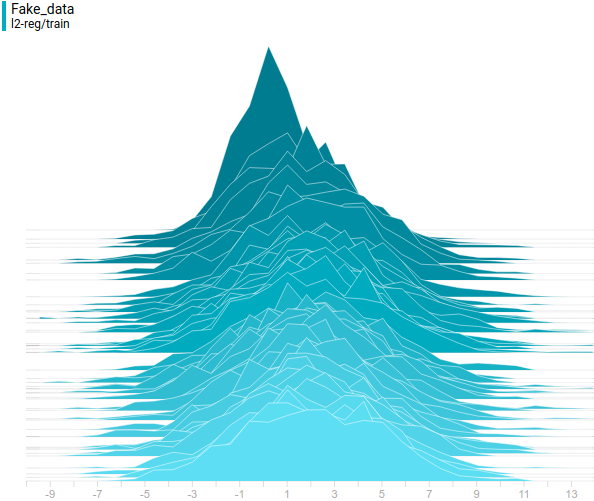
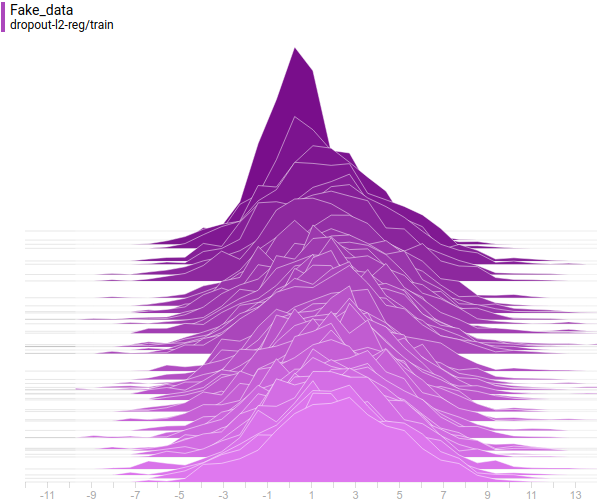
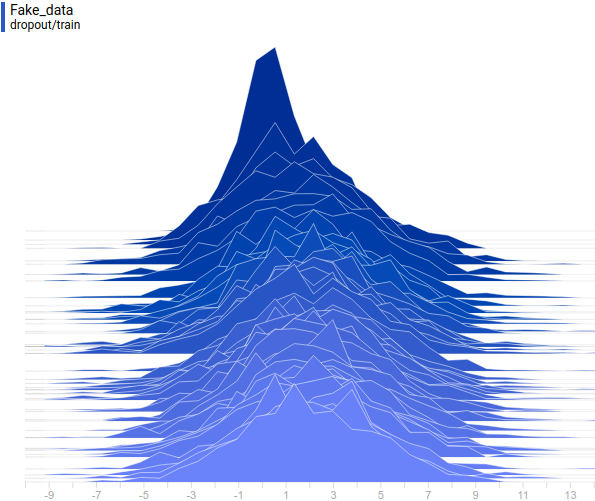
Давайте посмотрим на процесс обучения модели:
 |
Видно, что дискриминатор в начале обучения очень хорошо разделяет данные, но распределение генерируемых примеров очень быстро буквально “подползает” к распределению настоящих примеров. В конце концов, генератор настолько хорошо приближает данные, что дискриминатор становится константой $1/2$ и задача сходится.
Приближение смеси нормальных распределений I
Попробуем заменить $p(x)=N(\mu,\sigma)$ на $p(x)=Mixture(N(\mu_1, \sigma_1), N(\mu_2, \sigma_2))$, тем самым смоделировав мультимодальное распределение исходных данных. Для этой модели нужно изменить только код генерации реальных примеров. Вместо возвращения нормально распределенной случайной величины мы возвращаем смесь нескольких:
def data_batch(hparams):
count = len(hparams.input_mean)
componens = []
for i in range(count):
componens.append(
tf.contrib.distributions.Normal(
loc=hparams.input_mean[i],
scale=hparams.input_stddev[i]))
return tf.contrib.distributions.Mixture(
cat=tf.contrib.distributions.Categorical(
probs=[1./count] * count),
components=componens)
.sample(sample_shape=[hparams.batch_size, 1])
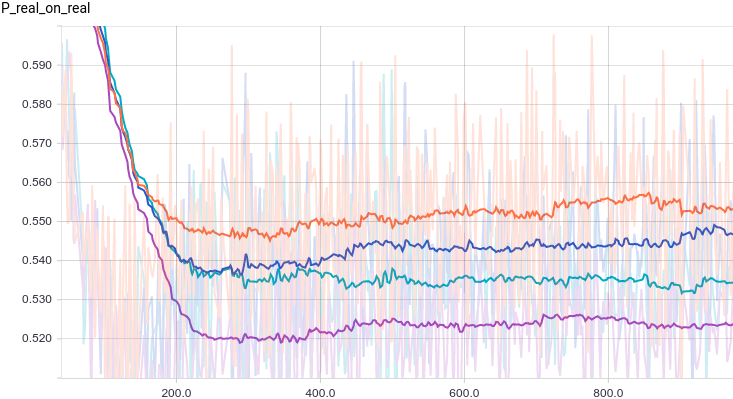
Ниже приведены графики для тех же самых моделей, что и в прошлом эксперименте, но для данных с двумя модами:
 |
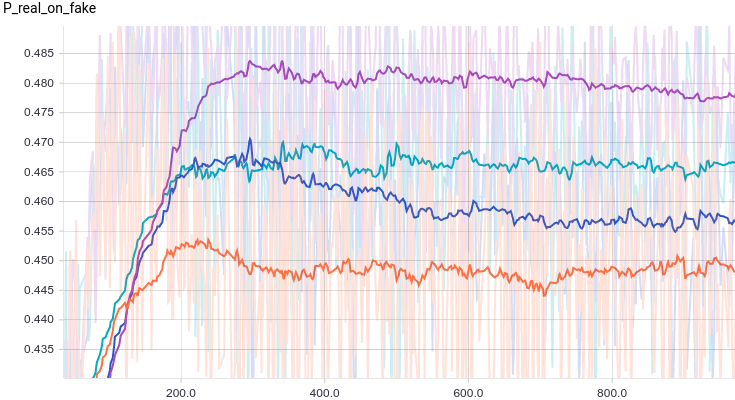 |
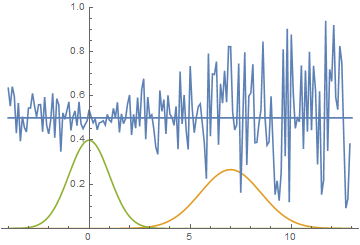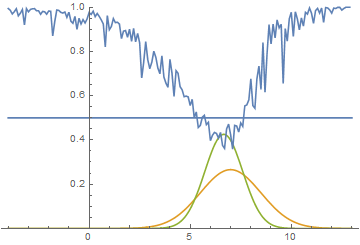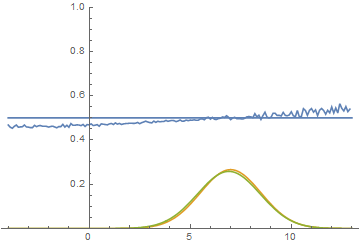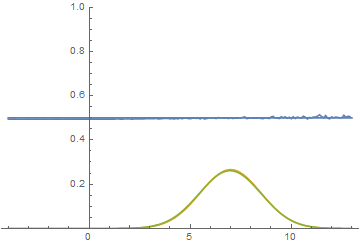
Интересно заметить, что регуляризованные модели показывают себя существенно лучше нерегуляризованных. Однако, независимо от модели видно, что теперь генератору не удается так хорошо обмануть дискриминатор. Давайте поймем, почему так получилось.
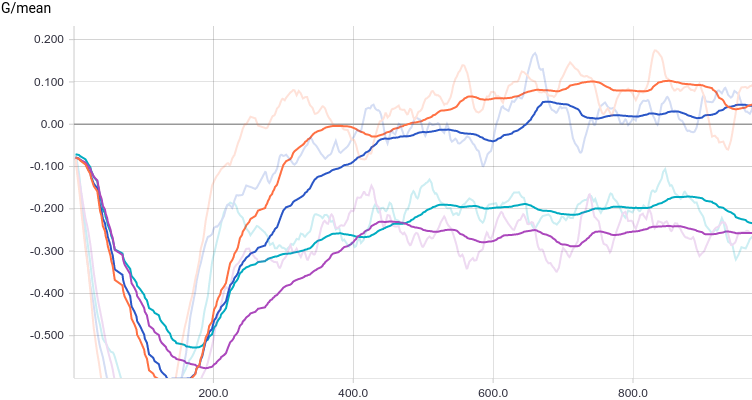 |
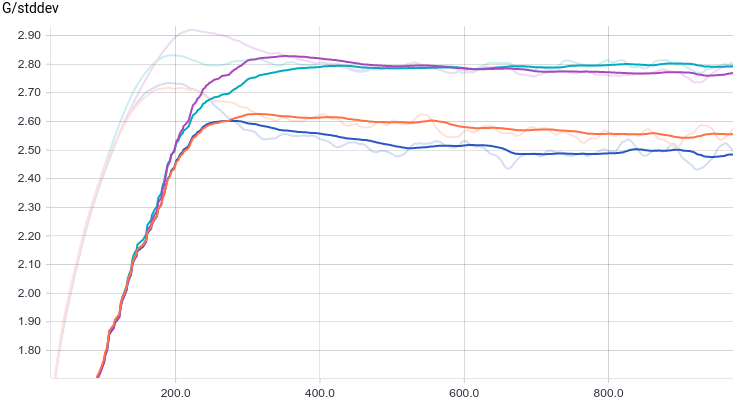 |
Как и в первом эксперименте, генератор приближает данные нормальным распределением. Причина снижения качества в том, что теперь данные нельзя точно приблизить нормальным распределением, ведь они сэмплируются из смеси двух нормальных. Моды смеси симметричны относительно нуля, и видно, что все четыре модели приближают данные нормальным распределением с центром рядом с нулем и достаточно большой дисперсией. Давайте посмотрим на распределения настоящих и поддельных примеров, чтобы понять, что происходит:
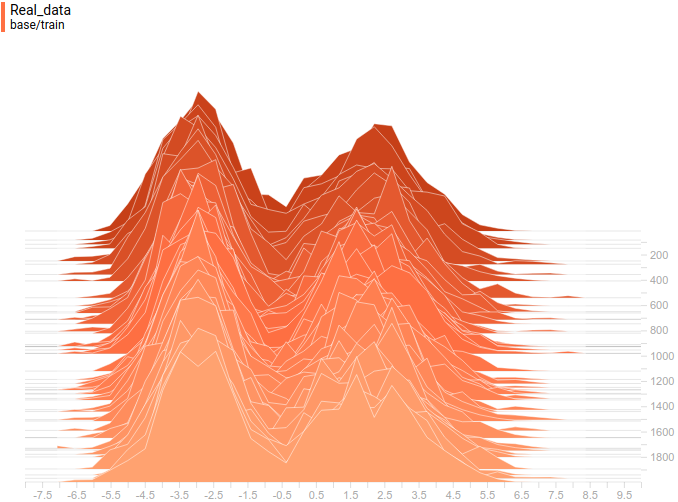 |
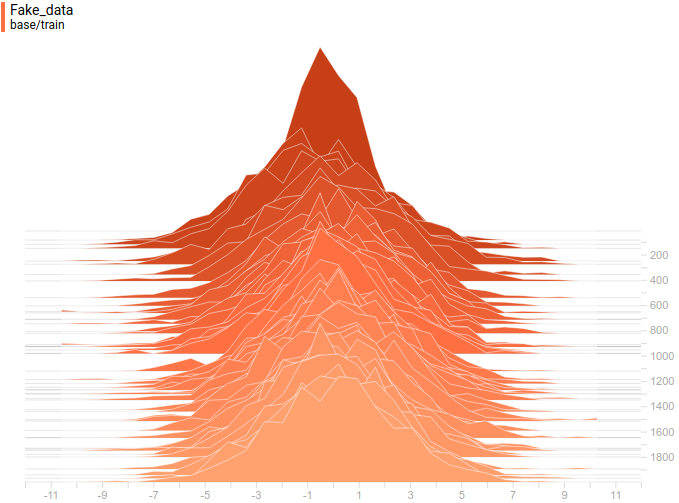 |
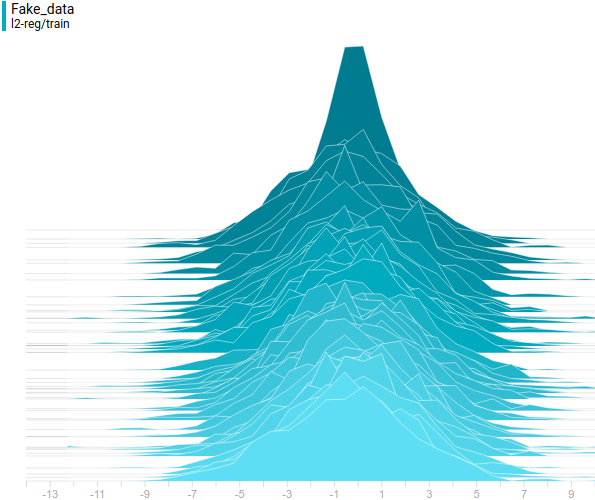
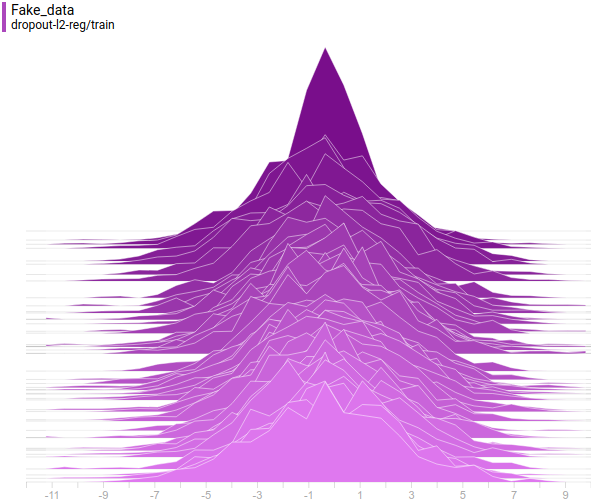
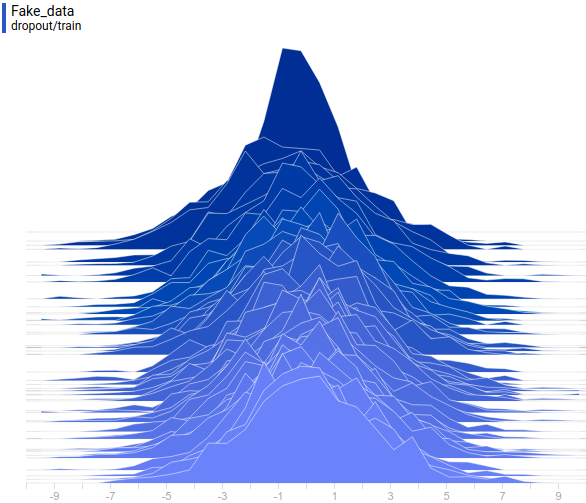
Так проходит процесс обучения модели:
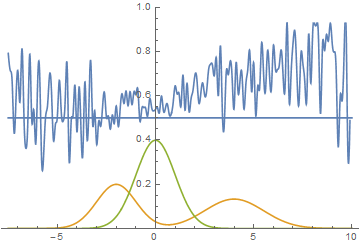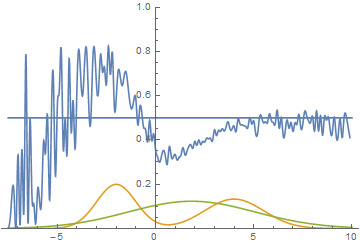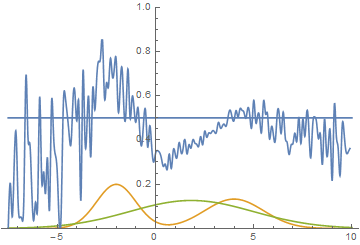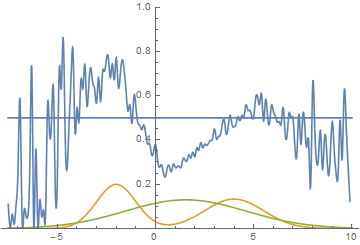 |
Эта анимация подробно показывает изученный выше случай. Генератор, не обладая достаточной экспрессивностью и имея возможность приближать данные только гауссианой, расплывается в широкую гауссиану, пытаясь охватить обе моды распределения данных. В результате генератор достоверно обманывает дискриминатор только в местах, где площади под кривыми генератора и исходных данных близки, то есть в районе пересечений этих кривых.
Однако, это не единственный возможный случай. Давайте подвинем правую моду еще немного правее, чтобы начальное приближение генератора ее не захватывало.
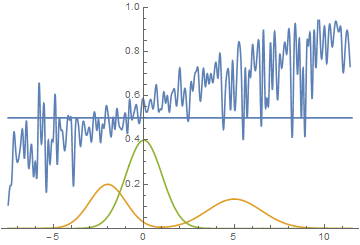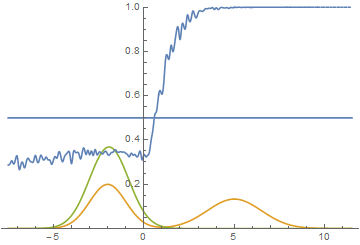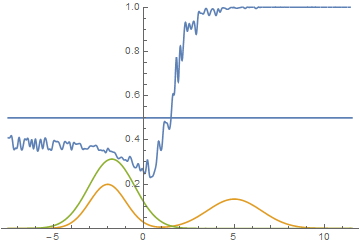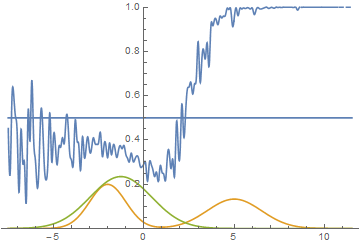 |
Видно, что в этом случае генератору выгоднее всего попытаться приблизить левую моду распределения. После того, как это происходит, генератор пытается предпринять попытки захватить и левую моду. Это выглядит, как осцилляции стандартного отклонения генератора во второй половине анимации. Но все эти попытки проваливаются, так как дискриминатор как-бы “запирает” генератор и для захвата левой моды ему необходимо преодолеть барьер из высокой функции потерь, чего он не может сделать из-за недостаточно большой скорости обучения. Данный эффект называется коллапсированием моды.
На двух вышеописанных примерах мы увидели два типа проблем, возникающих в том случае, если генератор недостаточно мощный, чтобы выразить исходное распределение данных: усреднение мод, когда генератор приближает все распределение, но везде достаточно плохо; и коллапсирование моды, когда генератор выучивает подмножество мод, а те, которые он не выучил, никак на него не влияют.
Помимо того, что обе этих проблемы приводят к несходимости дискриминатора к $1/2$, они также приводят к снижению качества генеративной модели. Первая проблема приводит к тому, что генератор выдает примеры “между” мод, которых не должно быть, вторая проблема приводит к тому, что генератор выдает примеры только из некоторых мод, тем самым снижая богатство исходного распределения данных.
Приближение смеси нормальных распределений II
Причиной того, что в предыдущем разделе не получилось до конца обмануть дискриминатор была тривиальность генератора, который просто делал линейное преобразование. Попробуем теперь в качестве генератора использовать полносвязную трехслойную нейронную сеть:
def generator(self, input, hparams):
# Первый полносвязный слой с 256 фичами.
input_size = 1
features = 256
weights = tf.get_variable(
"weights_1", initializer=tf.truncated_normal(
[input_size, features], stddev=0.1))
biases = tf.get_variable(
"biases_1", initializer=tf.constant(0.1, shape=[features]))
hidden_layer = tf.nn.relu(tf.matmul(input, weights) + biases)
# Второй полносвязный слой с 256 фичами.
features = 256
weights = tf.get_variable(
"weights_2", initializer=tf.truncated_normal(
[input_size, features], stddev=0.1))
biases = tf.get_variable(
"biases_2", initializer=tf.constant(0.1, shape=[features]))
hidden_layer = tf.nn.relu(tf.matmul(input, weights) + biases)
# Последний линейный слой, генерирующий пример.
output_size = 1
weights = tf.get_variable(
"weights_out", initializer=tf.truncated_normal(
[features, output_size], stddev=0.1))
biases = tf.get_variable(
"biases_out",
initializer=tf.constant(0.1, shape=[output_size]))
return tf.matmul(hidden_layer, weights) + biases
Давайте посмотрим на графики обучения.
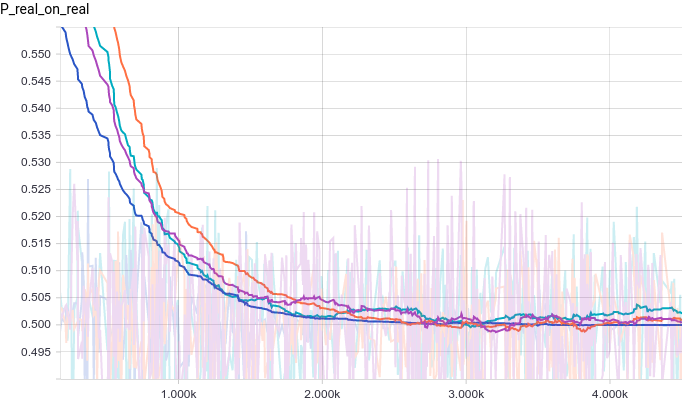 |
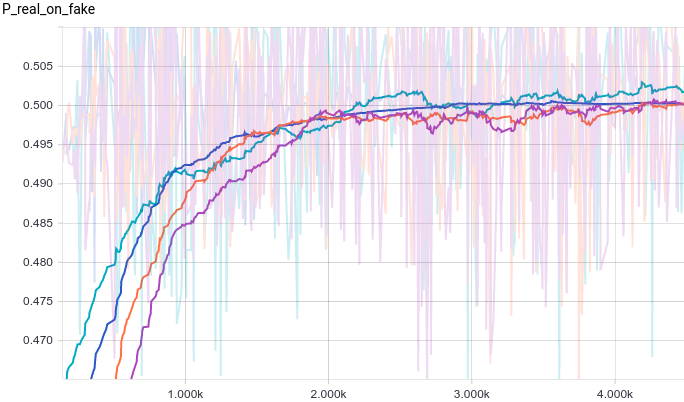 |
Видно, что из-за большого количества параметров обучение стало гораздо более шумным. Дискриминаторы всех моделей сходятся к результату около $1/2$, но ведут себя нестабильно вокруг этой точки. Давайте посмотрим на форму генератора.
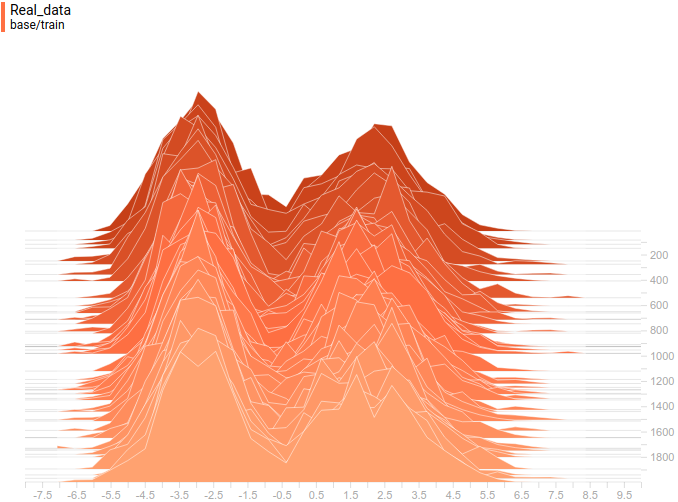 |
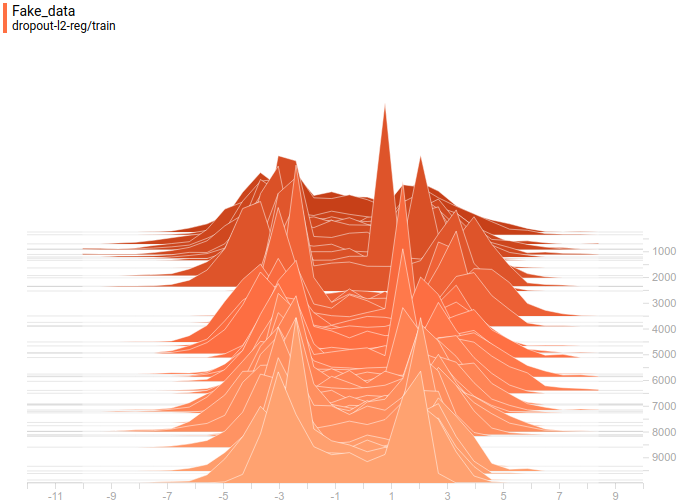 |
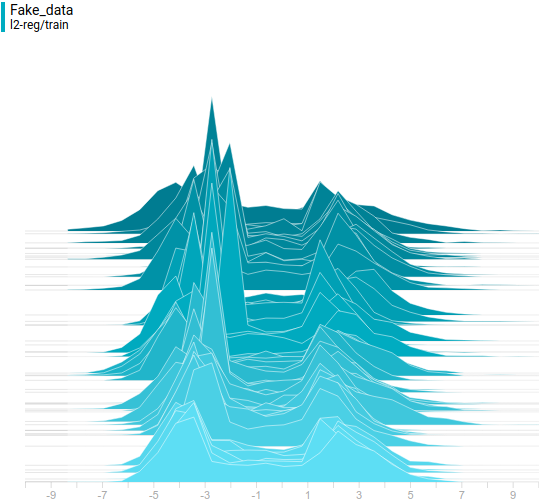
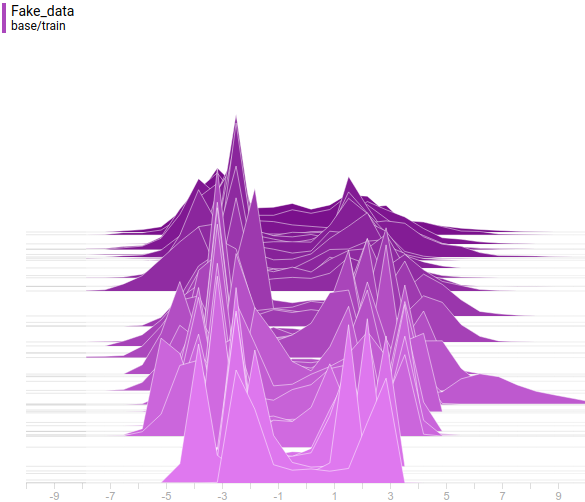
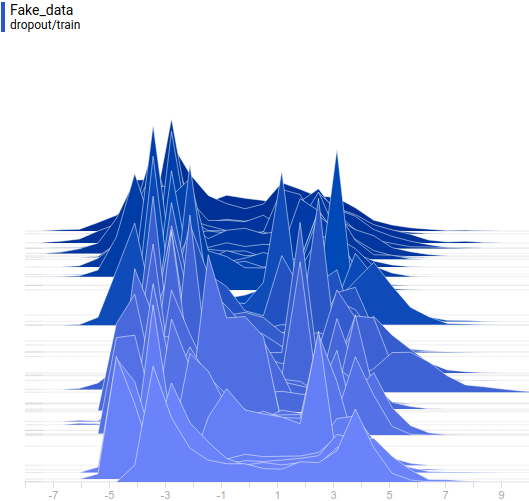
Видно, что распределение генератора хоть не совпадает с распределением данных, но достаточно сильно похоже на него. Самая регуляризованная модель опять показала себя лучше всех. Видно, что она выучила две моды, примерно совпадающие с модами распределения данных. Размеры пиков тоже не очень точно, но приближают распределение данных. Таким образом, нейросетевой генератор способен выучить мультимодальное распределение данных.
Так проходит процесс обучения модели:
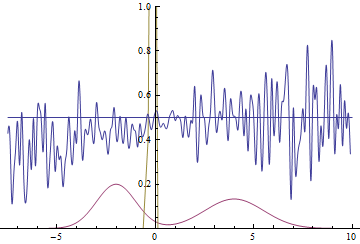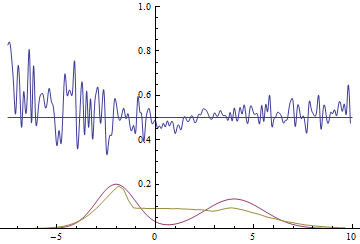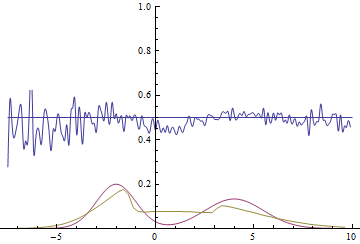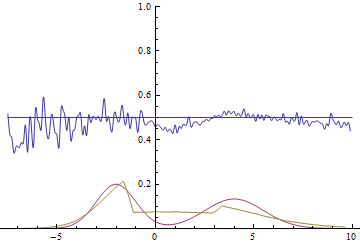 |
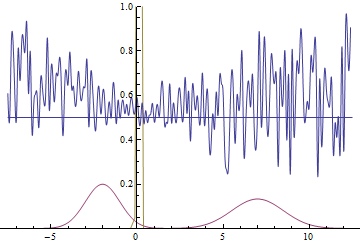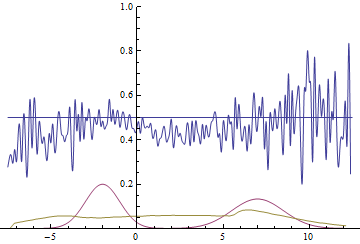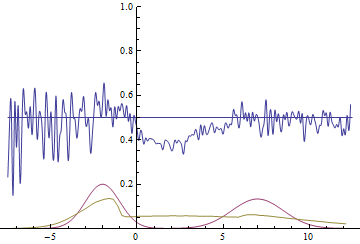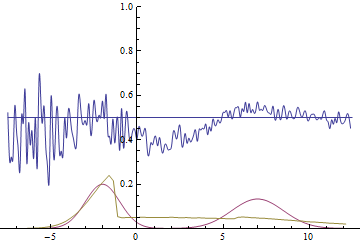 |
Эти две анимации показывают обучение на распределениях данных из предыдущего раздела. Из этих анимаций видно, что при использовании достаточно большого генератора с множеством параметров он, пусть и довольно грубо, но способен приближать мультимодальное распределение, тем самым косвенно подтверждая то, что проблемы из предыдущего раздела возникают из-за недостаточно сложного генератора. Дискриминаторы на этих анимациях гораздо более шумные, чем в разделе про нахождение параметров нормального распределения, но, тем не менее, к концу обучения начинают напоминать зашумленную горизонтальную прямую $D(x)=1/2$.
Итоги
GAN — это модель, для приближения произвольного распределения только с помощью сэмплирования из этого распределения. В этой статье мы посмотрели в деталях, как модель работает на тривиальном примере поиска параметров нормального распределения и на более сложном примере аппроксимации бимодального распределения нейронной сетью. Обе задачи были с хорошей точностью решены, для чего потребовалось только использовать достаточно сложную модель генератора. В следующей статье мы перейдем от этих модельных примеров к реальным примерам генерации сэмплов из сложных распределений на примере распределения изображений.
Благодарности
Спасибо Olga Talanova и Ruslan Login за ревью текста. Спасибо Ruslan Login за помощь в подготовке изображений и анимаций. Спасибо Andrei Tarashkevich за помощь с версткой этой статьи.